4. Multivariate data - correlation tests

Overview

Teaching: 60 min
Exercises: 60 min

Questions

• How do we determine if two measured variables are significantly correlated?

Objectives

• Learn the basis for and application of correlation tests, including what their assumptions are and how significances are determined.

In this episode we will be using numpy, as well as matplotlib’s plotting library. Scipy contains an extensive range of distributions in its ‘scipy.stats’ library, so we will also need to import it. Remember: scipy modules should be installed separately as required - they cannot be called if only scipy is imported. We will also need to import the scipy.optimize library for some optimisation functions which we will use in this episode.

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sps
import scipy.optimize as spopt

Statistical properties of multivariate data

So far, we have considered statistical tests of univariate data by realising that the data themselves can be thought of as random variates. Many data sets consist of measurements of mutliple quantities, i.e. they are multivariate data. For example, optical measurements of a sample of galaxies may produce measurements of their distance, size, luminosity and metallicity for each galaxy.

For simplicity we will focus on a bivariate description in terms of variates \(X\) and \(Y\) which represent the measurements of two paired quantities (e.g. different quantities for a given object), although we will note how these generalise when including more variates.

Sample means, variances and errors on the mean

The sample means of each variate have the same meaning that they do in the univariate case considered in the previous episode. This is because the means can be separated via marginalisation over the other variable in their joint probability distributions, e.g.:

Since we know that the sample mean for a sample of \(n\) measurements \(x_{i}\), \(\bar{x}=\frac{1}{n}\sum\limits_{i=1}^{n} x_{i}\) is an unbiased estimator of the population mean, we can calculate the sample mean for any of the quantities we measure and use it for standard univariate tests such as the \(Z\)-test or \(t\)-test, to compare with a known population mean for that quantity, or means from other samples of that quantity.

The same arguments apply to the sample variance \(s^{2}_{x} = \frac{1}{n-1}\sum\limits_{i=1}^{n} (x_{i}-\mu)^{2}\) and sample standard deviations and standard errors on the mean (recalling that the latter two quantities have a small bias which can usually be safely ignored for large sample sizes).

Sample covariance and correlation coefficient

When we are studying multivariate data we can determine sample statistics for each variable separately as described above, but these do not tell us how the variables are related. For this purpose, we can calculate the sample covariance for two measured variables \(x\) and \(y\).:

where \(n\) is the number of pairs of measured data points \(x_{i}\), \(y_{i}\). The sample covariance is closely related to the sample variance (note the same Bessel’s correction), and when covariance is discussed you will sometimes see sample variance denoted as \(s_{xx}\). In fact, the covariance tells us the variance of the part of the variations which is linearly correlated between the two variables, just like the covariance for multivariate probability distributions of variates \(X\) and \(Y\), also known as the population covariance:

The sample covariance \(s_{xy}\) is an unbiased estimator of the population covariance \(\sigma_{xy}\), of the distribution which the measurements are sampled from. Therefore, if the two variables (i.e. the measured quantities) are independent, the expectation of the sample covariance is zero and the variables are also said to be uncorrelated. Positive and negative covariances, if they are statistically significant, correspond to correlated and anticorrelated data respectively. However, the strength of a correlation is hard to determine from covariance alone, since the amplitude of the covariance depends on the sample variance of the two variables, as well as the degree of linear correlation between them.

Therefore, just as with the population correlation coefficient we can normalise by the sample standard deviations of each variable to obtain the sample correlation coefficient, \(r\), also known as Pearson’s \(r\), after its developer:

The correlation coefficient gives us a way to compare the correlations for variables which have very different magnitudes. It is also an example of a test statistic, which can be used to test the hypothesis that the variables are uncorrelated, under certain assumptions.

Anscombe’s quartet

This collection of four graphs, known as Anscombe’s quartet, was first shown by statistician Francis J. Anscombe in a 1973 paper to demonstrate the importance of plotting and visual inspection of data, in addition to the computation of sample statistics. The quartet shows four hypothetical bivariate data sets, with each looking very different but all having the same sample means and variances (for both variables), Pearson correlation coefficients and linear regression parameters (see below). It’s clear that if we only calculated the sample statistics without actually plotting the data, we would miss vital information about some of the relationships. The conclusion from this exercise is: always plot your data!

Credit: Wikimedia Commons based on the figures shown in Anscombe, Francis J. (1973) Graphs in statistical analysis. American Statistician, 27, 17–21.

Correlation tests: Pearson’s r and Spearman’s rho

Besides Pearson’s \(r\), another commonly used correlation coefficient and test statistic for correlation tests is Spearman’s \(\rho\) (not to be confused with the population correlation coefficient which is also often denoted \(\rho\)), which is determined using the following algorithm:

1. Rank the data values \(x_{i}\), \(y_{i}\) separately in numerical order. Equal values in the sequence are assigned a rank equal to their average position, e.g. the 4th and 5th highest positions of the \(x_{i}\) have equal values and are given a rank 4.5 each. Note that the values are not reordered in \(i\) by this step, only ranks are assigned based on their numerical ordering.
2. For each pair of \(x_{i}\) and \(y_{i}\) a difference \(d_{i}=\mathrm{rank}(x_{i})-\mathrm{rank}(y_{i})\) is calculated.

3. Spearman’s \(\rho\) is calculated from the resulting rank differences:

   \[\rho = 1-\frac{6\sum^{n}_{i=1} d_{i}^{2}}{n(n^{2}-1)}\]

To assess the statistical significance of a correlation, \(r\) can be transformed to a new statistic \(t\):

or \(\rho\) can be transformed in a similar way:

Under the assumption that the data are i.i.d., meaning independent (i.e. no correlation) and identically distributed (i.e. for a given variable, all the data are drawn from the same distribution, although note that both variables do not have to follow this distribution), then provided the data set is large (approximately \(n> 500\)), \(t\) is distributed following a \(t\)-distribution with \(n-2\) degrees of freedom. This result follows from the central limit theorem, since the correlation coefficients are calculated from sums of random variates. As one might expect, the same distribution also applies for small (\(n<500\)) samples, if the data are themselves normally distributed, as well as being i.i.d..

The concept of being identically distributed means that each data point in one variable is drawn from the same population. This requires that, for example, if there is a bias in the sampling it is the same for all data points, i.e. the data are not made up of multiple samples with different biases.

Measurement of either correlation coefficient enables a comparison with the \(t\)-distribution and a \(p\)-value for the correlation coefficient to be calculated. When used in this way, the correlation coefficient can be used as a significance test for whether the data are consistent with following the assumptions (and therefore being uncorrelated) or not. Note that the significance depends on both the measured coefficient and the sample size, so for small samples even large \(r\) or \(\rho\) may not be significant, while for very large samples, even \(r\) or \(\rho\) which are close to zero could still indicate a significant correlation.

A very low \(p\)-value will imply either that there is a real correlation, or that the other assumptions underlying the test are not valid. The validity of these other assumptions, such as i.i.d., and normally distributed data for small sample sizes, can generally be assessed visually from the data distribution. However, sometimes data sets can be so large that even small deviations from these assumptions can produce spuriously significant correlations. In these cases, when the data set is very large, the correlation is (sometimes highly) significant, but \(r\) or \(\rho\) are themselves close to zero, great care must be taken to assess whether the assumptions underlying the test are valid or not.

Pearson or Spearman?

When deciding which correlation coefficient to use, Pearson’s \(r\) is designed to search for linear correlations in the data themselves, while Spearman’s \(\rho\) is suited to monotonically related data, even if the data are not linearly correlated. Spearman’s \(\rho\) is also better able to deal with large outliers in the tails of the data samples, since the contribution of these values to the correlation is limited by their ranks (i.e. irrespective of any large values the outlying data points may have).

Correlation tests with scipy

We can compute Pearson’s correlation coefficient \(r\) and Spearman’s correlation coefficient, \(\rho\), for bivariate data using the functions in scipy.stats. For both outputs, the first value is the correlation coefficient, the second the p-value. To start with, we will test this approach using randomly generated data (which we also plot on a scatter-plot).

First, we generate a set of \(x\)-values using normally distributed data. Next, we generate corresponding \(y\)-values by taking the \(x\)-values and adding another set of random normal variates of the same size (number of values). You can apply a scaling factor to the new set of random normal variates to change the scatter in the correlation. We will plot the simulated data as a scatter plot.

x = sps.norm.rvs(size=50)
y = x + 1.0*sps.norm.rvs(size=50)

plt.figure()
plt.scatter(x, y, c="red")
plt.xlabel("x", fontsize=14)
plt.ylabel("y", fontsize=14)
plt.tick_params(axis='x', labelsize=12)
plt.tick_params(axis='y', labelsize=12)
plt.show()

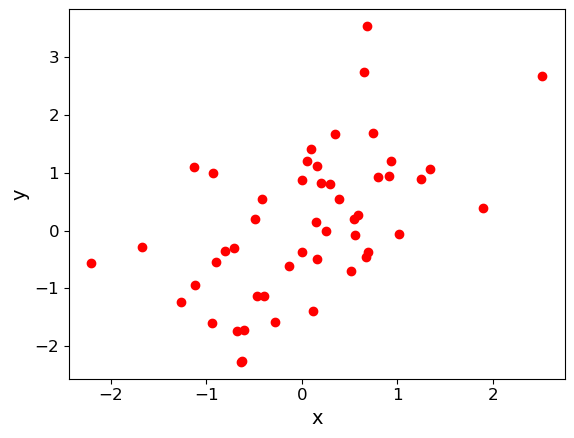
Finally, use the scipy.stats functions pearsonr and spearmanr to calculate and print the correlation coefficients and corresponding \(p\)-value of the correlation for both tests of the correlation. Since we know the data are normally distributed in both variables, the \(p\)-values should be reliable, even for \(n=50\). Try changing the relative scaling of the \(x\) and \(y\) random variates to make the scatter larger or smaller in your plot and see what happens to the correlation coefficients and \(p\)-values.

## Calculate Pearson's r and Spearman's rho for the data (x,y) and print them out, also plot the data.
(rcor, rpval) = sps.pearsonr(x,y)
(rhocor, rhopval) = sps.spearmanr(x,y)

print("Pearson's r and p-value:",rcor, rpval)
print("Spearman's rho and p-value:",rhocor, rhopval)

For the example data plotted above, this gives:

Pearson's r and p-value: 0.5358536492516484 6.062792564158924e-05
Spearman's rho and p-value: 0.5417046818727491 4.851710819096097e-05

Note that the two methods give different values (including for the \(p\)-value). How can this be? Surely the data are correlated or they are not, with a certain probability? It is important to bear in mind that (as in all statistical tests) we are not really asking the question “Are the data correlated?” rather we are asking: assuming that the data are really uncorrelated, independent and identically distributed, what is the probability that we would see such a non-zero absolute value of this particular test-statistic by chance? \(r\) and \(\rho\) are different test-statistics: they are optimised in different ways to spot deviations from random uncorrelated data.

Programming example: comparing the effects of outliers on Pearson’s \(r\) and Spearman’s \(\rho\)

Let’s look at this difference between the two methods in more detail. What happens when our data has certain properties, which might favour or disfavour one of the methods?

Let us consider the case where there is a cloud of data points with no underlying correlation, plus an extreme outlier (as might be expected from some error in the experiment or data recording). You may remember something like this as one of the four cases from ‘Anscombe’s quartet’.

First generate the random data: use the normal distribution to generate 50 data points which are uncorrelated between x and y and then replace one with an outlier which implies a correlation, similar to that seen in Anscombe’s quartet. Plot the data, and measure Pearson’s \(r\) and Spearman’s \(\rho\) coefficients and \(p\)-values, and compare them - how are the results of the two methods different in this case? Why do you think this is?

Solution

x = sps.norm.rvs(size=50)
y = sps.norm.rvs(size=50)
x[49] = 10.0
y[49] = 10.0

## Now plot the data and compare Pearson's r and Spearman's rho and the associated p-values

plt.figure()
plt.scatter(x, y, c="red",s=10)
plt.xlabel("x", fontsize=20)
plt.ylabel("y", fontsize=20)
plt.tick_params(axis='x', labelsize=20)
plt.tick_params(axis='y', labelsize=20)
plt.show()

(rcor, rpval) = sps.pearsonr(x,y)
(rhocor, rhopval) = sps.spearmanr(x,y)

print("Pearson's r and p-value:",rcor, rpval)
print("Spearman's rho and p-value:",rhocor, rhopval)

Key Points

• The sample covariance between two variables is an unbiased estimator for population covariance and shows the part of variance that is produced by linearly related variations in both variables.

• Normalising the sample covariance by the product of the sample standard deviations of both variables, yields Pearson’s correlation coefficient, r.

• Spearman’s rho correlation coefficient is based on the correlation in the ranking of variables, not their absolute values, so is more robust to outliers than Pearson’s coefficient.

• By assuming that the data are independent (and thus uncorrelated) and identically distributed, significance tests can be carried out on the hypothesis of no correlation, provided the sample is large (\(n>500\)) and/or is normally distributed.