Introducing probability distributions

Overview

Teaching: 30 min
Exercises: 10 min

Questions

• How are probability distributions defined and described?

Objectives

• Learn how the pdf, cdf, quantiles, ppf are defined and how to plot them using scipy.stats distribution functions and methods.

In this episode we will be using numpy, as well as matplotlib’s plotting library. Scipy contains an extensive range of distributions in its ‘scipy.stats’ module, so we will also need to import it. Remember: scipy modules should be installed separately as required - they cannot be called if only scipy is imported.

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sps

Michelson’s speed-of-light data is a form of random variable. Clearly the measurements are close to the true value of the speed of light in air, to within <0.1 per cent, but they are distributed randomly about some average which may not even be the true value (e.g. due to systematic error in the measurements).

We can gain further understanding by realising that random variables do not just take on any value - they are drawn from some probability distribution. In probability theory, a random measurement (or even a set of measurements) is an event which occurs (is ‘drawn’) with a fixed probability, assuming that the experiment is fixed and the underlying distribution being measured does not change over time (statistically we say that the random process is stationary).

The cdf and pdf of a probability distribution

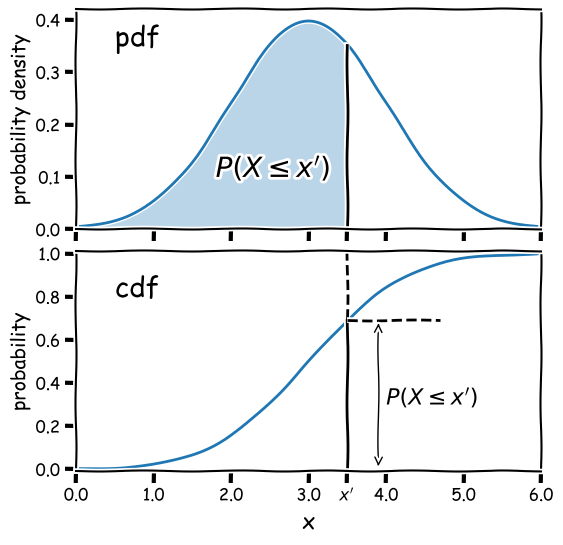
Consider a continuous random variable \(X\) (for example, a single measurement). For a fixed probability distribution over all possible values $x$, we can define the probability \(P\) that \(X\leq x\) as being the cumulative distribution function (or cdf), \(F(x)\):

We can choose the limiting values of our distribution, but since the variable must take on some value (i.e. the definition of an ‘event’ is that something must happen) it must satisfy:

\(\lim\limits_{x\rightarrow -\infty} F(x) = 0\) and \(\lim\limits_{x\rightarrow +\infty} F(x) = 1\)

From these definitions we find that the probability that \(X\) lies in the closed interval \([a,b]\) (note: a closed interval, denoted by square brackets, means that we include the endpoints \(a\) and \(b\)) is:

We can then take the limit of a very small interval \([x,x+\delta x]\) to define the probability density function (or pdf), \(p(x)\):

This means that the cdf is the integral of the pdf, e.g.:

where \(x^{\prime}\) is a dummy variable. The probability that \(X\) lies in the interval \([a,b]\) is:

and \(\int_{-\infty}^{\infty} p(x)\mathrm{d}x = 1\).

Why use the pdf?

By definition, the cdf can be used to directly calculate probabilities (which is very useful in statistical assessments of data), while the pdf only gives us the probability density for a specific value of \(X\). So why use the pdf? One of the main reasons is that it is generally much easier to calculate the pdf for a particular probability distribution, than it is to calculate the cdf, which requires integration (which may be analytically impossible in some cases!).

Also, the pdf gives the relative probabilities (or likelihoods) for particular values of \(X\) and the model parameters, allowing us to compare the relative likelihood of hypotheses where the model parameters are different. This principle is a cornerstone of statistical inference which we will come to later on.

Probability distributions: Uniform

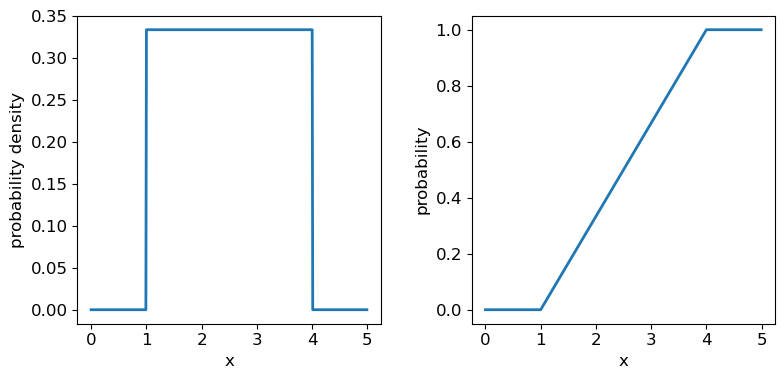
Now we’ll introduce two common probability distributions, and see how to use them in your Python data analysis. We start with the uniform distribution, which has equal probability values defined over some finite interval \([a,b]\) (and zero elsewhere). The pdf is given by:

where the notation \(p(x\vert a,b)\) means ‘probability density at x, conditional on model parameters \(a\) and \(b\)‘. The vertical line \(\vert\) meaning ‘conditional on’ (i.e. ‘given these existing conditions’) is notation from probability theory which we will use often in this course.

## define parameters for our uniform distribution
a = 1
b = 4
print("Uniform distribution with limits",a,"and",b,":")
## freeze the distribution for a given a and b
ud = sps.uniform(loc=a, scale=b-a) # The 2nd parameter is added to a to obtain the upper limit = b

Distribution parameters: location, scale and shape

As in the above example, it is often useful to ‘freeze’ a distribution by fixing its parameters and defining the frozen distribution as a new function, which saves repeating the parameters each time. The common format for arguments of scipy statistical distributions which represent distribution parameters, corresponds to statistical terminology for the parameters:

• A location parameter (the loc argument in the scipy function) determines the location of the distribution on the \(x\)-axis. Changing the location parameter just shifts the distribution along the \(x\)-axis.
• A scale parameter (the scale argument in the scipy function) determines the width or (more formally) the statistical dispersion of the distribution. Changing the scale parameter just stretches or shrinks the distribution along the \(x\)-axis but does not otherwise alter its shape.
• There may be one or more shape parameters (scipy function arguments may have different names specific to the distribution). These are parameters which do something other than shifting, or stretching/shrinking the distribution, i.e. they change the shape in some way.

Distributions may have all or just one of these parameters, depending on their form. For example, normal distributions are completely described by their location (the mean) and scale (the standard deviation), while exponential distributions (and the related discrete Poisson distribution) may be defined by a single parameter which sets their location as well as width. Some distributions use a rate parameter which is the reciprocal of the scale parameter (exponential/Poisson distributions are an example of this).

The uniform distribution has a scale parameter \(\lvert b-a \rvert\). This statistical distribution’s location parameter is formally the centre of the distribution, \((a+b)/2\), but for convenience the scipy uniform function uses \(a\) to place a bound on one side of the distribution. We can obtain and plot the pdf and cdf by applying those named methods to the scipy function. Note that we must also use a suitable function (e.g. numpy.arange) to create a sufficiently dense range of \(x\)-values to make the plots over.

## You can plot the probability density function
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(9,4))
# change the separation between the sub-plots:
fig.subplots_adjust(wspace=0.3)
x = np.arange(0., 5.0, 0.01)
ax1.plot(x, ud.pdf(x), lw=2)
## or you can plot the cumulative distribution function:
ax2.plot(x, ud.cdf(x), lw=2)
for ax in (ax1,ax2):
    ax.tick_params(labelsize=12)
    ax.set_xlabel("x", fontsize=12)
    ax.tick_params(axis='x', labelsize=12)
    ax.tick_params(axis='y', labelsize=12)
ax1.set_ylabel("probability density", fontsize=12)
ax2.set_ylabel("probability", fontsize=12)
plt.show()

Probability distributions: Normal

The normal distribution is one of the most important in statistical data analysis (for reasons which will become clear) and is also known to physicists and engineers as the Gaussian distribution. The distribution is defined by location parameter \(\mu\) (often just called the mean, but not to be confused with the mean of a statistical sample) and scale parameter \(\sigma\) (also called the standard deviation, but again not to be confused with the sample standard deviation). The pdf is given by:

It is also common to refer to the standard normal distribution which is the normal distribution with \(\mu=0\) and \(\sigma=1\):

The standard normal is important for many statistical results, including the approach of defining statistical significance in terms of the number of ‘sigmas’ which refers to the probability contained within a range \(\pm z\) on the standard normal distribution (we will discuss this in more detail when we discuss statistical significance testing).

Challenge: plotting the normal distribution

Now that you have seen the example of a uniform distribution, use the appropriate scipy.stats function to plot the pdf and cdf of the normal distribution, for a mean and standard deviation of your choice (you can freeze the distribution first if you wish, but it is not essential).

Solution

## Define mu and sigma:
mu = 2.0
sigma = 0.7
## Plot the probability density function
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(9,4))
fig.subplots_adjust(wspace=0.3)
## we will plot +/- 3 sigma on either side of the mean
x = np.arange(-1.0, 5.0, 0.01)
ax1.plot(x, sps.norm.pdf(x,loc=mu,scale=sigma), lw=2)
## and the cumulative distribution function:
ax2.plot(x, sps.norm.cdf(x,loc=mu,scale=sigma), lw=2)
for ax in (ax1,ax2):
    ax.tick_params(labelsize=12)
    ax.set_xlabel("x", fontsize=12)
    ax.tick_params(axis='x', labelsize=12)
    ax.tick_params(axis='y', labelsize=12)
ax1.set_ylabel("probability density", fontsize=12)
ax2.set_ylabel("probability", fontsize=12)
plt.show()

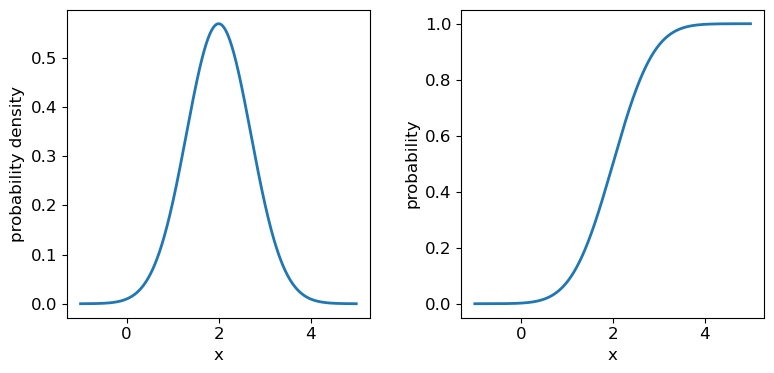
It’s useful to note that the pdf is much more distinctive for different functions than the cdf, which (because of how it is defined) always takes on a similar, slanted ‘S’-shape, hence there is some similarity in the form of cdf between the normal and uniform distributions, although their pdfs look radically different.

Quantiles

It is often useful to be able to calculate the quantiles (such as percentiles or quartiles) of a distribution, that is, what value of \(x\) corresponds to a fixed interval of integrated probability? We can obtain these from the inverse function of the cdf (\(F(x)\)). E.g. for the quantile \(\alpha\):

Note that \(F^{-1}\) denotes the inverse function of \(F\), not \(1/F\)! This is called the percent point function (or ppf). To obtain a given quantile for a distribution we can use the scipy.stats method ppf applied to the distribution function. For example:

## Print the 30th percentile of a normal distribution with mu = 3.5 and sigma=0.3
print("30th percentile:",sps.norm.ppf(0.3,loc=3.5,scale=0.3))
## Print the median (50th percentile) of the distribution
print("Median (via ppf):",sps.norm.ppf(0.5,loc=3.5,scale=0.3))
## There is also a median method to quickly return the median for a distribution:
print("Median (via median method):",sps.norm.median(loc=3.5,scale=0.3))

30th percentile: 3.342679846187588
Median (via ppf): 3.5
Median (via median method): 3.5

Intervals

It is sometimes useful to be able to quote an interval, containing some fraction of the probability (and usually centred on the median) as a ‘typical’ range expected for the random variable \(X\). We will discuss intervals on probability distributions further when we discuss confidence intervals on parameters. For now, we note that the .interval method can be used to obtain a given interval centred on the median. For example, the Interquartile Range (IQR) is often quoted as it marks the interval containing half the probability, between the upper and lower quartiles (i.e. from 0.25 to 0.75):

## Print the IQR for a normal distribution with mu = 3.5 and sigma=0.3
print("IQR:",sps.norm.interval(0.5,loc=3.5,scale=0.3))

IQR: (3.2976530749411754, 3.7023469250588246)

So for the normal distribution, with \(\mu=3.5\) and \(\sigma=0.3\), half of the probability is contained in the range \(3.5\pm0.202\) (to 3 decimal places).

Key Points

• Probability distributions show how random variables are distributed. Two common distributions are the uniform and normal distributions.

• Uniform and normal distributions and many associated functions can be accessed using scipy.stats.uniform and scipy.stats.norm respectively.

• The probability density function (pdf) shows the distribution of relative likelihood or frequency of different values of a random variable and can be accessed with the scipy statistical distribution’s pdf method.

• The cumulative distribution function (cdf) is the integral of the pdf and shows the cumulative probability for a variable to be equal to or less than a given value. It can be accessed with the scipy statistical distribution’s cdf method.

• Quantiles such as percentiles and quartiles give the values of the random variable which correspond to fixed probability intervals (e.g. of 1 per cent and 25 per cent respectively). They can be calculated for a distribution in scipy using the percentile or interval methods.

• The percent point function (ppf) (ppf method) is the inverse function of the cdf and shows the value of the random variable corresponding to a given quantile in its distribution.

• Probability distributions are defined by common types of parameter such as the location and scale parameters. Some distributions also include shape parameters.